BZOJ3144【HNOI2013】切糕 <最小割>

Problem

切糕

Description

经历千辛万苦小得到了一块切糕，切糕的形状是长方体，小打算拦腰将切糕切成两半分给小。出于美观考虑，小希望切面能尽量光滑且和谐。于是她找到你，希望你能帮她找出最好的切割方案。
出于简便考虑，我们将切糕视作一个长，宽，高的长方体点阵。我们将位于第层中第行，第列上的点称为，它有一个非负的不和谐值。一个合法的切面满足以下两个条件：

与每个纵轴有且仅有一个交点。即切面是一个函数，对于所有，，我们需指定一个切割点，且。
切面需要一定的光滑性要求，即相邻纵轴上的切割点不能相距太远。对于所有和，若，则 , 其中是给定的一个非负整数。

能有许多切面满足上面的条件，小希望找出总的切割点上的不和谐值最小的那个，即最小。

Input

第一行是三个正整数，表示切糕的长、宽、高。第二行有一个非负整数，表示光滑性要求。接下来是个行列的矩阵，第个矩阵的第行第列是。
的数据满足，，且给出的所有的不和谐值不超过。

Output

仅包含一个整数，表示在合法基础上最小的总不和谐值。

Sample Input

Sample Output

Hint

最佳切面的为

标签：网络流 最小割

Solution

建模神题。
建图：
建层，每层的图，相邻两竖边建模如下

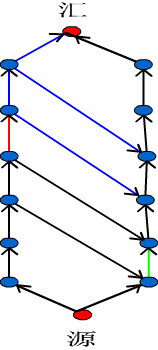
(图片转载自Zarxdy34)
这样如果割掉红边，右边割的边必须在绿边下面才能有流。所以割的边就限制在绿边上面了。因此这样一来，下界就满足了。
对于上界，右边的几个点反过来同种方式建边（图中只画了左侧的边）

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define MAX_A 40
#define MAX_N 70000
#define MAX_M 300000
#define INF 2147483647
using namespace std;
int s, t, id[MAX_A+5][MAX_A+5][MAX_A+5];
int move[2][4] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
struct Edge {int v, c, nxt;} E[MAX_M+5];
int pre[MAX_N+5], d[MAX_N+5], cnt, num;
queue <int> que;
void init() {cnt = num = 0; memset(pre, -1, sizeof(pre));}
void insert(int u, int v, int c) {
    E[cnt].v = v, E[cnt].c = c;
    E[cnt].nxt = pre[u], pre[u] = cnt++;
    E[cnt].v = u, E[cnt].c = 0;
    E[cnt].nxt = pre[v], pre[v] = cnt++;
}
bool BFS() {
    memset(d, -1, sizeof(d));
    while (!que.empty())	que.pop();
    d[s] = 0, que.push(s);
    while (!que.empty()) {
        int u = que.front();
        for (int i = pre[u]; i != -1; i = E[i].nxt)
            if (E[i].c && d[E[i].v] == -1)
                d[E[i].v] = d[u]+1, que.push(E[i].v);
        que.pop();
    }
    return d[t] != -1;
}
int DFS(int u, int flow) {
    if (u == t)	return flow;
    int ret = 0;
    for (int i = pre[u]; i != -1; i = E[i].nxt) {
        int v = E[i].v;
        if (E[i].c && d[u]+1 == d[v]) {
            int tmp = DFS(v, min(flow, E[i].c));
            E[i].c -= tmp, E[i^1].c += tmp;
            flow -= tmp, ret += tmp;
            if (!flow)	break;
        }
    }
    if (!ret)	d[u] = -1;
    return ret;
}
int Dinic() {
    int ret = 0;
    while (BFS())	ret += DFS(s, INF);
    return ret;
}
int main() {
    init();
    int a, b, h, d;	scanf("%d%d%d%d", &a, &b, &h, &d);
    for (int i = 1; i <= h+1; i++)
        for (int j = 1; j <= a; j++)
            for (int k = 1; k <= b; k++)
                id[i][j][k] = ++num;
    s = 0, t = ++num;
    for (int j = 1; j <= a; j++)
        for (int k = 1; k <= b; k++)
            insert(s, id[1][j][k], INF), 
            insert(id[h+1][j][k], t, INF);
    for (int i = 1; i <= h; i++)
        for (int j = 1; j <= a; j++)
            for (int k = 1; k <= b; k++) {
                int c;	scanf("%d", &c);
                insert(id[i][j][k], id[i+1][j][k], c);
            }
    for (int i = d+1; i <= h+1; i++)
        for (int j = 1; j <= a; j++)
            for (int k = 1; k <= b; k++) {
                int x, y;
                for (int l = 0; l < 4; l++)
                    if (id[i][x = j+move[0][l]][y = k+move[1][l]])
                        insert(id[i][j][k], id[i-d][x][y], INF);
            }
    printf("%d", Dinic());
    return 0;
}